Уравнение тока в колебательном контуре

Рассмотрим колебательный контур, который помимо , и , содержит внешнюю переменную ЭДС .За положительное направление обхода выберем, например, направление по ходу часовой стрелке (рис.1).

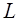
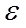
Ток считается положительным, если течет по контуру в положительном направлении, и отрицательным – в противоположном направлении.

Токи считаются квазистационарными (мгновенные значения тока практически одинаковы на всех участках цепи), что позволяет использовать формулы для статических полей, в частности закон Ома.

Обозначим через 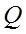заряд той из обкладок конденсатора, направление которой к другой обкладке совпадает с положительным направлением обхода.

Закон Ома для участка цепи :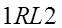

(1)

где ЭДС самоиндукции 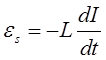(катушка считается недеформируемой и не имеющей ферромагнитного сердечника), а разность потенциалов . Тогда уравнение (1) примет вид:

(2)

Учитывая, что и , получим уравнение колебательного контура:

(3)

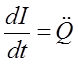
Уравнение колебательного контура(3) может быть представлено в виде:

(4)

где (5)

— коэффициент затухания;

(6)

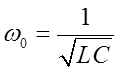
— собственная частота колебательного контура.

При (в контуре отсутствует внешняя ЭДС) электрические колебания являются свободными, при — незатухающими, при -затухающими.

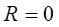
Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9990 — | 7783 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

«Физика — 11 класс»

Уравнение, описывающее процессы в колебательном контуре

Есть колебательный контур, сопротивлением R которого можно пренебречь.

Уравнение, описывающее свободные электрические колебания в контуре, можно получить с помощью закона сохранения энергии.
Полная электромагнитная энергия W контура в любой момент времени равна сумме его энергий магнитного и электрического полей:

Полная энергия не меняется с течением времени, если сопротивление R контура равно нулю, тогда производная полной энергии по времени равна нулю.
Следовательно, равна нулю сумма производных по времени от энергий магнитного и электрического полей:

Физический смысл вышеприведенного уравнения состоит в том, что скорость изменения энергии магнитного поля по модулю равна скорости изменения энергии электрического поля.
Знак «—» указывает на то, что, когда энергия электрического поля возрастает, энергия магнитного поля убывает (и наоборот).

После вычисления производных в уравнении, получается

Производная заряда по времени представляет собой силу тока в данный момент времени:

Производная силы тока по времени есть не что иное, как вторая производная заряда по времени, подобно тому как производная скорости по времени (ускорение) есть вторая производная координаты по времени.
Тогда основное уравнение, описывающее свободные электрические колебания в контуре:

Полученное уравнение ничем, кроме обозначений, не отличается от уравнения, описывающего колебания пружинного маятника.

Период свободных колебаний в контуре

Формула Томсона
В основном уравнении коэффициент представляет собой квадрат циклической частоты для свободных электрических колебаний:

Период свободных колебаний в контуре, таким образом, равен:

Эта формула называется формулой Томсона в честь английского физика У. Томсона (Кельвина), который ее впервые вывел.

Период свободных колебаний зависит от L и С.
При увеличении индуктивности L ток медленнее нарастает со временем и медленнее падает до нуля.
А чем больше емкость С, тем большее время требуется для перезарядки конденсатора.

Гармонические колебания заряда и тока.

Координата при механических колебаниях изменяется со временем по гармоническому закону:

Заряд конденсатора меняется с течением времени по такому же закону:

где
q_m — амплитуда колебаний заряда.

Сила тока также совершает гармонические колебания:

где
I_m = q_mω₀ — амплитуда колебаний силы тока.
Колебания силы тока опережают по фазе на колебания заряда.

Точно так же колебания скорости тела в случае пружинного или математического маятника опережают на колебания координаты (смещения) этого тела.

В действительности, из-за неизбежного наличия сопротивления электрической цепи, колебания будут затухающими.
Сопротивление R также будет влиять и на период колебаний, чем больше сопротивление, тем бо́льшим будет период колебаний.
При достаточно большом сопротивлении колебания совсем не возникнут.
Конденсатор разрядится, но перезарядки его не произойдет, энергия электрического и магнитного полей перейдет в тепло.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика

Колебательный контур — замкнутая электрическая цепь, состоящая из включенных последовательно катушки индуктивности L, конденсатора емкостью С и резистора сопротивлением R.

Колебательный контур предназначен для возбуждения и поддержания электромагнитных колебаний. В идеализированном колебательном контуре сопротивлением резистора пренебрегают (рис. 5.10, а; К —> 0).

Свободные электромагнитные колебания — периодически повторяющиеся изменения электрического заряда, силы тока и разности потенциалов, происходящие в колебательном контуре за счет сообщенной этому контуру энергии, которая в дальнейшем не пополняется.

Если ключ К находится в положении 1, конденсатор заряжается (рис. 5.10, б). В положении 2 конденсатор начинает разряжаться и в цепи появится ток, периодически меняющийся по

амплитуде и направлению, т. е. в контуре возникают свободные электромагнитные волны.

Последовательные стадии колебательного процесса в контуре и аналогия между электромагнитными и механическими колебаниями представлены на рис. 5.11. В процессе этих колебаний через каждые четверть периода колебаний происходит периодическое превращение энергии электрического поля конденсатора в энергию магнитного поля катушки (и наоборот).

На рис. 5.11 приняты обозначения: q_m, I_m, U_m — соответственно амплитудные значения электрического заряда, силы тока и напряжения; ?_эл и Е_магн — максимальная энергия электрического и магнитного полей; Е_{к тах} и Е_{п тах} — максимальные кинетическая и потенциальная энергии маятника при гармонических колебаниях.

Уравнение свободных электромагнитных колебаний в контуре без активного сопротивления:

где оо₀ =1/(VZC) — собственная частота контура; его решение

г Д е Чтах — амплитуда колебаний заряда.

Период свободных незатухающих колебаний (формула Томсона):

В реальных колебательных контурах активное сопротивление R —»• 0, поэтому свободные электромагнитные колебания всегда являются колебаниями затухающими.

Сила тока в колебательном контуре равна производной от заряда q по времени t:

где /_тах = co₀q_max — амплитуда силы тока.

Колебания силы тока контуре опережают по фазе на ^ колебания заряда (рис. 5. 12).

Напряжение на конденсаторе:

где U_max = q_max/C — амплитуда напряжения.

Из приведенного выражения следует, что колебания напряжения совпадают по фазе с колебаниями заряда.

Энергия магнитного поля катушки:

Энергия электрического поля конденсатора:

Полная электромагнитная энергия W колебательного контура:

где I и q — сила тока и заряд в любой момент времени.

Переменный электрический ток. Активное, емкостное и индуктивное сопротивления в цепи гармонического тока

Переменный ток — ток, изменяющийся во времени по гармоническому закону. Обычно под переменным током понимают периодический ток, в котором средние за период значения силы тока и напряжения равны нулю.

Переменный ток представляет собой вынужденные электромагнитные колебания, происходящие с частотой со, совпадающей с частотой вынуждающего напряжения. Переменное напряжение вырабатывается на электростанциях.

Действующие (эффективные) значения тока и напряжения:

где U_m и 1_т — амплитудные значения напряжения и силы тока.

Амперметры и вольтметры градуируются по действующим значениям тока и напряжения.