На векторных диаграммах можно выделить прямоугольный треугольник напряжений.
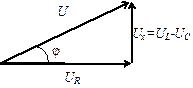 Рис. 18 Рис. 18 |
По теореме Пифагора можно установить связь между полным напряжением цепи и напряжениями на ее отдельных участках:
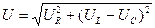
Если разделить стороны треугольника напряжений на ток (в цепи с последовательным соединением элементов ток одинаков во всех участках), то (в соответствии с законом Ома) получим треугольник сопротивлений.
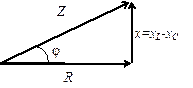 Рис. 19 Рис. 19 |
Здесь х = xL — xC — реактивное сопротивление цепи, а Z — полное сопротивление цепи:
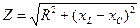
Полученное уравнение устанавливает связь межу различными сопротивлениями цепи.
Если умножить стороны треугольника напряжений на ток, то получим треугольник мощностей:
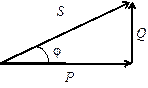 Рис. 20 Рис. 20 |
Здесь Р = URI — активная мощность, которая выделяется на активных сопротивления цепи. Она связана с необратимыми преобразованиями электрической энергии, то есть с совершением работы в электроустановке. Активная мощность измеряется в ваттах [Вт].
Q = UxI — реактивная мощность. Связана в электроустановках с совершением обратимых преобразований энергии, работы она не совершает. В электроустановках затрачивается на создание электрических (С) и магнитных (L) полей. Реактивная мощность измеряется вольт амперах реактивных [вар].
S = UI — полная мощность, измеряется в вольт амперах [В*А]. Из треугольника мощностей определим:
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9848 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Цифровое представление динамических процессов затрудняет восприятие, усложняет расчет выходных параметров после изменения условий на входе или в результате выполненной обработки. Векторная диаграмма токов и напряжений помогает успешно решать обозначенные задачи. Ознакомление с теорией и практическими примерами поможет освоить данную технологию.
- Разновидности векторных диаграмм
- Векторные диаграммы и комплексное представление
- Примеры применения
- Механика, гармонический осциллятор
- Свободные гармонические колебания без затухания
- Гармонический осциллятор с затуханием и внешней вынуждающей силой
- Расчет электрических цепей
- Преобразование Фурье
- Сложение двух синусоидальных колебаний
- Фурье-образ прямоугольного сигнала
- Дифракция
- Построение векторной диаграммы напряжений и токов
- Видео
Разновидности векторных диаграмм
Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.
С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.
Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.
Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.
Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.
Векторные диаграммы и комплексное представление
Такой инструментарий помогает строить наглядные графические схемы колебательных процессов. Аналогичный результат обеспечивает применение комплексных числовых выражений. В этом варианте, кроме оси с действительными, применяют дополнительный координатный отрезок с мнимыми значениями. Для представления вектора пользуются формулой A*ei(wt+f0), где:
- А – длина;
- W – угловая скорость;
- f0 – начальный угол.
Значение действительной части равно A*cos*(w*t+f0). Это выражение описывает типичное гармоническое колебание с базовыми характеристиками.
Примеры применения
В следующих разделах приведены описания задач, которые решают с помощью представленной методики. Следует подчеркнуть, что применение комплексных чисел пригодно для сложных расчетов с высокой точностью. Однако на практике достаточно часто сравнительно простой векторной графики с наглядным отображением исходной информации на одном рисунке.
Механика, гармонический осциллятор
Таким термином обозначают устройство, которое можно вывести из равновесного состояния. После этого система возвращается в сторону исходного положения, причем сила (F) соответствующего воздействия зависит от дальности первичного перемещения (d) прямо пропорционально. Величину ее можно уточнить с помощью постоянного корректирующего коэффициента (k). Отмеченные определения связаны формулой F=-d*k
К сведению. Аналогичные процессы происходят в системах иной природы. Пример – создание аналога на основе электротехнического колебательного контура (последовательного или параллельного). Формулы остаются теми же с заменой соответствующих параметров.
Свободные гармонические колебания без затухания
Продолжая изучение темы на примерах механических процессов, можно отметить возможность построения двухмерной схемы. Скорость в этом случае на оси Х отображается так же, как и в одномерном варианте. Однако здесь можно учесть дополнительно фактор ускорения, которое направляют под углом 90° к предыдущему вектору.
Гармонический осциллятор с затуханием и внешней вынуждающей силой
В этом случае также можно воспользоваться для изучения взаимного влияния дополнительных факторов векторной графикой. Как и в предыдущем примере, скорость и другие величины представляют в двухмерном виде. Чтобы правильно моделировать процесс, проверяют суммарное воздействие внешних сил. Его направляют к центру системы (точке равновесия). С применением геометрических формул вычисляют амплитуду механических колебаний после начального воздействия с учетом коэффициента затухания и других значимых факторов.
Расчет электрических цепей
Векторную графику применяют для сравнительно несложных цепей, которые созданы из набора элементов линейной категории: конденсаторы, резисторы, катушки индуктивности. Для более сложных схем пользуются методикой расчета «Комплексных амплитуд», в которой реактивные компоненты определяют с помощью импедансов.
Векторная диаграмма в данном случае выполняет функцию вспомогательного чертежа, который упрощает решение геометрических задач. Для катушек и конденсаторов, чтобы не пользоваться комплексным исчислением, вводят специальный термин – реактивное сопротивление. При синусоидальном токе изменение напряжения на индуктивном элементе описывается формулой U=-L*w*I0sin(w*t+f0).
Несложно увидеть подобие с классическим законом Ома. Однако в данном примере изменяется фаза. По этому параметру на конденсаторе напряжение отстает от тока на 90°. В индуктивности – обратное распределение. Эти особенности учитывают при размещении векторов на рисунке. В формуле учитывается частота, которая оказывает влияние на величину этого элемента.
Преобразование Фурье
Векторные технологии применяют для анализа спектров радиосигналов в определенном диапазоне. Несмотря на простоту методики, она вполне подходит для получения достаточно точных результатов.
Сложение двух синусоидальных колебаний
В ходе изучения таких источников сигналов рекомендуется работать со сравнительно небольшой разницей частот. Это поможет создать график в удобном для пользователя масштабе.
Фурье-образ прямоугольного сигнала
В этом примере оперируют суммой синусоидальных сигналов. Последовательное сложение векторов образует многоугольник, вращающийся вокруг единой точки. Для правильных расчетов следует учитывать отличия непрерывного и дискретного распределения спектра.
Дифракция
Для этого случая пользуются тем же отображением отдельных синусоид в виде векторов, как и в предыдущем примере. Суммарное значение также вписывается в окружность.
Построение векторной диаграммы напряжений и токов
Для изучения технологии выберем однофазный источник синусоидального напряжения (U). Ток изменяется по формуле I=Im*cos w*t. Подключенная цепь содержит последовательно подключенные компоненты со следующими значениями:
- резистор: Ur=Im*R*cos w*t;
- конденсатор: Uc=Im*Rc*cos (w*t-π/2), Rc=1/w*C;
- катушка: UL= Im*RL*cos(w*t+π/2), RL=w*L.
При прохождении по цепи переменного тока на реактивных элементах будет соответствующий сдвиг фаз. Чтобы построить вектора правильно, рассчитывают амплитуды и учитывают изменение направлений. Ниже приведена последовательность создания графики вручную.
Далее с применением элементарных правил геометрии проверяют взаимное влияние векторов.
На первом рисунке приведен результат сложения двух векторов при условии, когда Uc меньше UL. Добавив значение на сопротивление, получим результирующее напряжение Um. На третьей иллюстрации отмечен общий фазовый сдвиг.
В топографической диаграмме начало координат совмещают с так называемой точкой «нулевого потенциала». Такое решение упрощает изучение отдельных участков сложных схем.
В интернете можно найти программу для построения векторных диаграмм в режиме online.
Видео
Наверняка при решении задач по электротехнике многие сталкивались с некоторыми сложностями в построении векторных диаграмм. Начнем с определения векторной диаграммы.
Векторная диаграмма — это изображение синусоидально изменяющихся величин в виде векторов на плоскости.
Векторные диаграммы применяют потому, что сложение и вычитание синусоидальных величин, неизбежные при расчете цепей переменного тока, наиболее просто выполняются в векторной форме. Кроме того векторные диаграммы отличаются простотой и наглядностью.
Построение векторной диаграммы выполняется в прямоугольной плоскости. Чтобы построить диаграмму нужно провести вектор длиною равный амплитудному значению искомой величины, под углом сдвига относительно другой величины. Возможно, вы не сразу поймете смысл сказанного, для этого нужно изучить пример.
В качестве примера рассмотрим построение векторной диаграммы для цепи, состоящей из последовательно подключенных конденсатора, резистора и катушки. Напряжение на катушке UL=15 В, напряжение на конденсаторе UC=20 В, напряжение на резисторе UR=10 В, ток в цепи I=3 А. Требуется найти общее напряжение.
Катушка носит индуктивный характер, а значит, в ней напряжение опережает ток по фазе на 90°.
Конденсатор носит емкостной характер, значит, ток в нем опережает по фазе напряжение на 90°.
Резистор обладает только активным сопротивлением, и напряжение в нем совпадает по фазе с током.
Итак, для начала отложим вектор тока в масштабе. Масштаб для тока у нас будет 1 А/см.
Теперь отложим вектор напряжения на катушке, масштаб для напряжения возьмем 5 В/см, получается, что нужно отложить шесть клеток вверх, так как напряжение в катушке опережает ток. Для наглядности обозначим синим цветом.
Далее мы будем откладывать вектор активного сопротивления, так как напряжение в одной фазе с током, то мы его откладываем из конца вектора UL параллельно вектору тока I. Обозначим его красным цветом.
Следующим шагом отложим вектор напряжения на конденсаторе, так как оно запаздывает на 90°, мы его отложим вертикально вниз, из конца вектора U R . Обозначим желтым цветом.
И последним этапом мы отложим вектор общего напряжения, из начала координат в конец вектора UC и обозначим его зеленым цветом.
Общее напряжение получилось равным 2,23 В, причем характер цепи емкостной, так как напряжение отстает от тока.
Аналогичным образом выполняется построение векторной диаграммы токов.






